A stacked addition problem demonstrating carrying. "839 + 445 = 1284" Space below the problem displays "hint," "done," "previous," and "next" buttons.

Apprentice Learner: Artificial Intelligence (AI) in the Classroom

by

by Sarah Hampton

One of my favorite things about CIRCLS is the opportunity to collaborate with education researchers and technology developers. Our goal as a community is to innovate education using technology and the learning sciences to give more learners engaging educational experiences to help them gain deep understanding. To reach that goal, we need expertise from many areas: researchers who study how we learn best, teachers who understand how new technologies can be integrated, and developers who turn ideas into hardware or software.

Recently I’ve been reminded of an opportunity when Judi, Pati, and I meet with Daniel Weitekemp in June of 2020. Daniel, a PhD student at Carnegie Mellon University at the time, was developing an AI tool for teachers called Apprentice Learner.

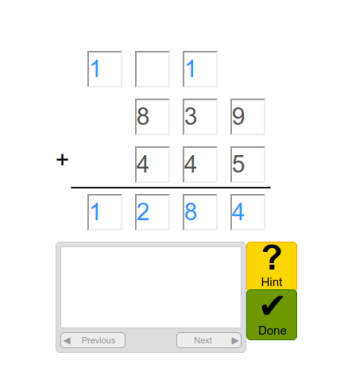
A stacked addition problem demonstrating carrying. "839 + 445 = 1284" Space below the problem displays "hint," "done," "previous," and "next" buttons.

Figure 1. Apprentice Learner Interface that students use when interacting with Apprentice Learner. The user can request a hint or type in their answer and then hit done.

Apprentice Learner looks a bit like a calculator at first glance, so an onlooker might be tempted to say, “What’s so cutting edge about this? We’ve been able to do basic math on calculators for years.” But we need to understand the difference between traditional software and software using artificial intelligence (AI) to appreciate the new benefits this kind of tool can bring to the education table.

In a basic calculator, there’s an unchanging program that tells the screen to display “1284” when you type in “839+445.” There’s no explanation given for how and why the programming behind a calculator works. Yet, for each math problem someone could type in a calculator, there is an answer that has been explicitly programmed to be displayed on the screen.

Contrast a calculator to Apprentice Learner, which uses machine learning (a type of artificial intelligence). No one tells Apprentice Learner to display “1284” when it sees 839+445.” Instead, it has some basic explicit instructions and is given lots of examples of correctly solved problems adding 2 or more columns of numbers. Then it has to figure out how to answer new questions. The examples it is given are called training data. In this case, Apprentice Learner was given explicit instructions about adding single digit numbers and then lots of training data–multidigit addition problems with their answers–maybe problems like “21+43=64,” “49+8=57,” and “234+1767=2001.” Then, it starts guessing at ways to arrive at the answers given from the training data.

The first guess might be to stack the numbers and add each column from left to right. That works perfectly for “21+43,” but gives an incorrect answer of “129” for “49+8.”

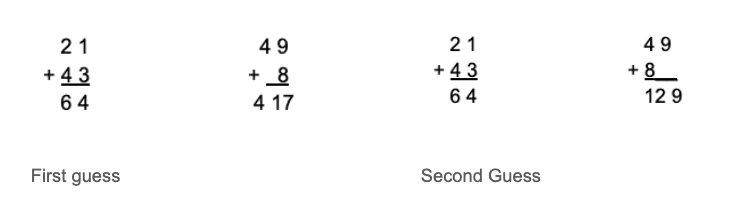
Two guesses. First: “21 correctly stacked over 43 which equals 64. The next stacked equation gives an incorrect answer of “129” for “49+8” stack because the computer calculates 4+8 in the first column and brings the 9 in the second column down. Second: “21 correctly stacked over 43 which equals 64. The next stacked equation gives an incorrect answer of “417” for “49+8” stack because the computer calculates 4 for column 1 and 17 for column 2 and puts them together.

The second guess might be to stack the numbers and add each column from right to left. Again, that works perfectly for “21+43.” Unfortunately, that would give an answer of “417” for “49+8.”

The software continues finding patterns and trying out models until it finds one that fits the training data best. You can see below that, eventually, Apprentice Learner “figured out” how to regroup (aka carry) so it could arrive at the correct answer.

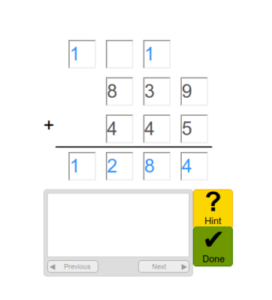
A stacked addition problem demonstrating carrying. "839 + 445 = 1284" Space below the problem displays "hint," "done," "previous," and "next" buttons.

So what are the implications for something like this in education? Here are a few of my thoughts:

Apprentice Learner models inductive learning which can help pre-service teachers.

Induction is the process of establishing a general law by observing multiple specific examples. It’s the basic principle machine learning uses. In addition, inductive reasoning tasks such as identifying similarities and differences, pattern recognition, generalization, and hypothesis generation play important roles when learning mathematics. (See Haverty, Koedinger, Klahr, Alibali). Multiple studies have shown that greater learning occurs when students induce mathematical principles themselves first rather than having the principles directly explained at the onset. (See Zhu and Simon, Klauer, and Koedinger and Anderson)

However, instructional strategies that promote students to reason inductively prior to direct instruction can be difficult for math teachers to implement if they haven’t experienced learning math this way themselves. Based on conversations with multiple math teacher colleagues throughout the years, most of us learned math in more direct manners i.e., the teacher shows and explains the procedure first and then the learner imitates it with practice problems. (Note: even this language communicates that there is “one right way” to do math unlike induction in which all procedures are evaluated for usefulness. This could be a post in its own right.)

Apprentice Learner could provide a low-stakes experience to encourage early-career teachers to think through math solutions inductively. Helping teachers recognize and honor multiple student pathways to a solution empowers students, helps foster critical thinking, and increases long-term retention. (See Atta, Ayaz, and Nawaz and Pokharel) This could also help teachers preempt student misconceptions (like column misalignment caused by a misunderstanding of place values and digits) and be ready with counterexamples to show why those misconceptions won’t work for every instance, much like I demonstrated above with Apprentice Learner’s possible first and second guess at how multi-digit addition works. Ken Koedinger, professor of human-computer interaction and psychology at CMU put it like this, “The machine learning system often stumbles in the same places that students do. As you’re teaching the computer, we can imagine a teacher may get new insights about what’s hard to learn because the machine has trouble learning it.”

The right training data is crucial.
What would have happened if there were only some types of problems in the training data? What if they were all two digit numbers? Then it wouldn’t have mattered if you stacked them left to right or right to left. What if none required regrouping/carrying? Then adding right to left is a perfectly acceptable way to add in every instance. But when all the edge cases are included, the model is more accurate and robust.

Making sure the training data has enough data and a wide array of data to cover all the edge cases is crucial to the success of any AI model. Consider what has already happened when insufficient training data was used for facial recognition software. “A growing body of research exposes divergent error rates across demographic groups, with the poorest accuracy consistently found in subjects who are female, Black, and 18-30 years old.” Some of the most historically excluded people were most at risk for negative consequences of the AI failing. What’s important for us as educators? We need to ask questions about things like training data before using AI tools, and do our best to protect all students from negative consequences of software.

Feedback is incredibly advantageous.

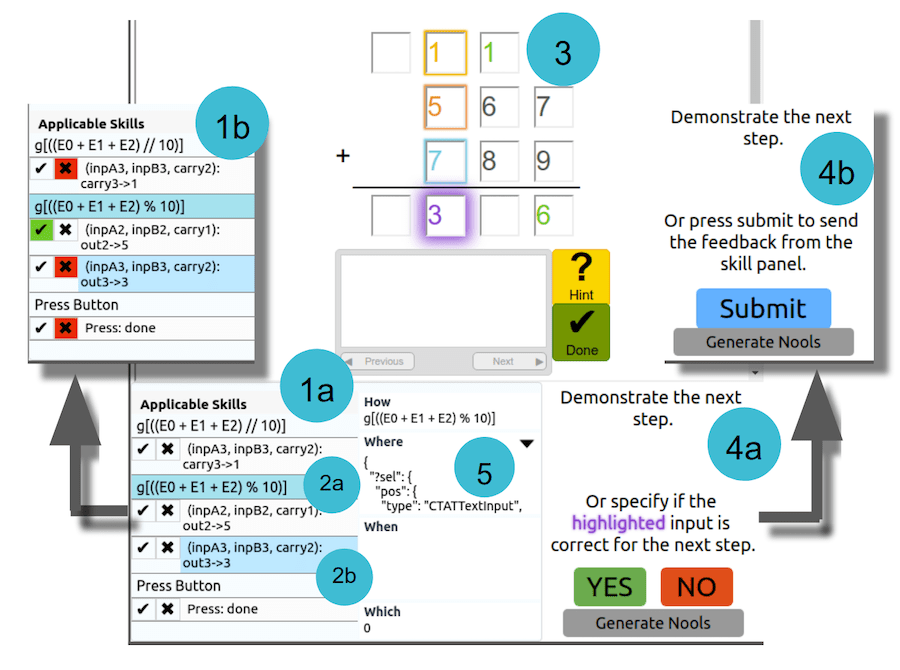
A flowchart demonstrating different ways a user can give direct input to Apprentice Learner such as demonstrating the next step, specifying if the highlighted input is correct, etc.

Figure 2. Diagram of how it works to give feedback to the Apprentice Learner system.

One of the most interesting things about Apprentice Learner is how it incorporates human feedback while it develops models. Instead of letting the AI run its course after the initial programming, it’s designed for human interaction throughout the process. The developers’ novel approach allows Apprentice Learner to be up and running in about a fourth of the time compared to similar systems. That’s a significant difference! (You can read about their approach in the Association for Computing Machinery’s Digital Library.)

It’s no surprise that feedback helps the system learn, in fact, there’s a parallel between helping the software learn and helping students learn. Feedback is one of the most effective instructional strategies in our teacher toolkit. As I highlighted in a former post, feedback had an average effect size of 0.79 standard deviation – an effect greater than students’ prior cognitive ability, socioeconomic background, and reduced class size on students’ performance. I’ve seen firsthand how quickly students can learn when they’re given clear individualized feedback exactly when they need it. I wasn’t surprised to see that human intervention could do the same for the software.

I really enjoyed our conversation with Daniel. It was interesting to hear our different perspectives around the same tool. (Judi is a research scientist, Pati is a former teacher and current research scientist, Daniel is a developer, and I am a classroom teacher.) I could see how this type of collaboration during the research and development of tools could amplify their impacts in classrooms. We always want to hear from more classroom teachers! Tweet @EducatorCIRCLS and be part of the conversation.

Thank you for your time in talking and reviewing this post, Daniel Weitekamp, PhD Candidate, Carnegie Mellon University.

Learn More about Apprentice Learner:

Learn More about Math Teaching and Learning:

Educator CIRCLS posts are licensed under a Creative Commons Attribution 4.0 International License. If you use content from this site, please cite the post and consider adding: “Used under a Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/).”
Suggested citation format: [Authors] ([Year]). [Title]. Educator CIRCLS Blog. Retrieved from [URL]